О волновых процессах света и их использовании в фотографии

Все рассмотренные фотографические процессы и все практические приемы, известные фотолюбителям, основаны только на одном свойстве света - его воздействии на светочувствительную эмульсию. Под воздействием световых лучей в эмульсии образуется скрытое изображение, которое с помощью проявителя переводится в видимое изображение. Для образования этого изображения, т. е. локальных потемнений, пропорциональных интенсивности света в той или иной точке фотоэмульсии, используется лишь суммарная энергия света, усредненная за некоторый промежуток времени. Волновая природа света при этом никак не используется и не влияет на режим фотосъемки.

Хотя такой принцип работы более ста лет служит фундаментом классической фотографии, он не является единственным способом регистрации изображений. Умелое использование волновой природы света открывает необычайные возможности перед фотографией.

В течение долгого времени крупнейшие физики спорили и различным образом объясняли природу света. Одни считали, что свет это поток частиц, а другие говорили, что свет это волна. Теорию света как поток частиц - корпускул - излагал Ньютон, а первым, кто выдвинул волновую теорию света, был Гюйгенс [10], но спор продолжался.

И все же волновые свойства света были практически обнаружены и наглядно показаны еще в 1802 году Юнгом. Поскольку световые колебания непосредственно наблюдать невозможно, Юнг нашел способ доказать их существование косвенным путем. Для понимания материала, изложенного далее в этой книге, необходимо вспомнить основные понятия в области волновых процессов. Начнем с самого наглядного примера.

Что такое волна? Чтобы ответить на этот вопрос, необходимо вспомнить, как бегут волны по полю спелой ржи под порывами ветра. Мы хорошо видим поступательное движение этих волн, но отлично знаем, что каждый стебель ржи остается на месте. Так что же движется? Особенностью процесса здесь является то, что движется не вещество, а состояние вещества. Колоски только качаются на стеблях. Если взять другой пример - волны на воде, то и здесь частицы воды движутся вверх и вниз, а волна, пробегающая по поверхности пруда или бассейна, не является движением воды в направлении движения волны. Оба вида упомянутых волн являются только лишь моделями процессов где движется не само вещество, а энергия, распространяющаяся в веществе. Это правило о движении одной лишь энергии не зависит от вида среды, в которой она распространяется, т. е. распространение механической энергии в виде волы на воде, или звуковых волн в воздухе, или электромагнитных световых волн в пространстве - все это распространение энергии, а не среды, и все это волновые процессы.

Бросим на спокойную, зеркально-гладкую поверхность воды бассейна небольшой камушек. На поверхности воды образуются расходящиеся кругами волны, которые движутся от источника (места падения камушка) во все стороны с определенной скоростью. Одним из важных параметров этого процесса является длина волны, обозначаемая буквой λ, т. е. расстояние между двумя соседними гребнями волн; расстояние между средними точками волны, как показано на рис. 29, называют периодом волны и обозначают T.

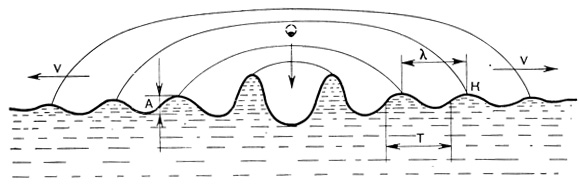
Рис. 29. Пример образования волн на поверхности воды и их основные параметры

Если в точке K, положение которой неизменно относительно краев бассейна, отмечать прохождение гребней волн, то можно заметить, что, чем больше расстояние между гребнями волн, тем реже гребни будут проходить через эту точку. Частота прохождения гребней через точку K и есть частота колебаний, обозначаемая обычно буквой f. Очевидно, чем больше скорость распространения υ, тем больше будет частота f, а чем больше длина волны λ, тем меньше будет частота при том же значении υ. Высоту гребня волны относительно впадины, обозначенную на рис. 29 буквой A, называют амплитудой колебаний. Очевидно, что, если мы бросим в воду не маленький, а большой камень, амплитуда будет больше, чем в первом случае.

Бросая камушки в воду и присматриваясь к происходящим волновым процессам, можно установить некоторые их особенности. Так, круговая волна пересекает бассейн приблизительно за одно и то же время при повторении опыта, если условия бросания камушков одинаковы. Из этого следует, что скорость распространения волн постоянна для данной среды. Действительно, волны на водной поверхности распространяются настолько медленно, что мы без напряжения прослеживаем взглядом их движение. Колебания воздуха, т. е. звуковые колебания, распространяются со скоростью свыше 965 км/ч, а световые колебания имеют скорость примерно 300 000 км/с. Приведенный пример определения одного из физических параметров колебательного процесса показывает, что даже примитивный инструмент исследования (бассейн и камушки) может быть полезным в наглядном представлении других параметров, которые нам необходимо понять при рассмотрении принципа цветной фотографии Липпмана и рассматриваемой далее голографии.

Весьма важным параметром волнового процесса является фаза колебаний. Воспроизведем этот параметр в бассейне. Разделим бассейн так, чтобы волны не влияли друг на друга, для чего установим в воде перегородку, выступающую над поверхностью воды. Бросим в каждую часть бассейна по камушку, чтобы возбудить две волны. При этом оба камушка бросим в одно и то же место относительно стенок бассейна. Кроме того, один камушек бросим чуть-чуть позже другого.

На рис. 30 показаны обе волны, причем круговые гребни волны от первого камушка показаны сплошными линиями, а круговые гребни другой волны от брошенного позже камушка показаны пунктирными линиями. Выберем произвольную точку на перегородке, разделяющей бассейн. Очевидно, поскольку скорость распространения волн в бассейне постоянна и одинакова для обеих частей бассейна, гребень второй волны от запоздавшего камушка будет проходить через эту точку тоже с некоторым запаздыванием. Это запаздывание называют фазой и обозначают буквой φ. На рис. 30 справа показан профиль обеих волн в плоскости перегородки. Если рассматривают две таких волны совместно, о них говорят! "Волны имеют сдвиг по фазе".

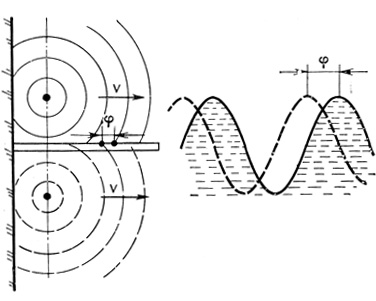
Рис. 30. Схема, поясняющая образование фазового сдвига в волновых процессах

Рассмотрим теперь явление интерференции волн [11], Интерференцией называют явление, возникающее при наложении двух или более световых волн. При этом в различных точках пространства происходит усиление или ослабление результирующей амплитуды световых колебаний в зависимости от соотношения между фазами колебаний волн в этих точках. Наибольшая величина амплитуды, равная сумме амплитуд обеих волн, достигается при разности фаз, равной периоду волны. Наименьшая величина амплитуды волны, равная разности амплитуд обеих волн, достигается при разности фаз, равной половине периода. Оба эти случая изображены на рис. 31. Наиболее четкая картина интерференции наблюдается при равенстве амплитуд, поскольку результирующая амплитуда будет либо равна удвоенной амплитуде, либо нулю. Если же амплитуды интерферирующих волн неодинаковы, то суммарные амплитуды имеют какие-то средние значения между нулем и удвоенной амплитудой. Этот случай также показан на рис. 31. Интерференцию волн можно наблюдать в бассейне, если бросить на поверхность воды сразу два камушка рядом. Круговые волны, пересекаясь, будут интерферировать.

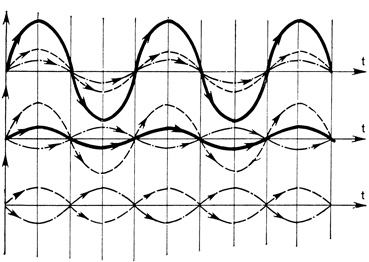
Рис. 31. Схема интерференции волн в различных случаях

Именно с помощью интерференции Юнг подтвердил волновую природу света. В настоящее время используются оптические приборы, основанные на интерференции света, их называют интерферометрами. С помощью такого прибора создают стоячие световые волны [11].

Стоячие волны возникают вследствие интерференции двух бегущих волн равной частоты, распространяющихся в противоположных направлениях, т. е. навстречу друг другу. Для получения встречного движения световых волн используют зеркала. В этом случае отраженная волна налагается на прямую и происходят их интерференция, причем не только частота, но и амплитуда оказывается одинаковой.

На рис. 32 показана интерференция таких волн и образование стоячей волны. В начальный момент времени разность фаз прямой и отраженной волн равна половине периода, поэтому волны гасят друг друга. В некоторые моменты времени сдвиг по фазе будет равен нулю, и амплитуда волн сложится, т. е. удвоится. В других случаях будут получены промежуточные значения амплитуд. Таким образом, две бегущие навстречу друг другу световые волны порождают стационарную картину, т. е. волна останавливается и может в течение длительного времени оставаться неподвижной. Гребень стоячей волны называют пучностью, а точку, где амплитуда стоячей волны имеет нулевое значение, узлом.

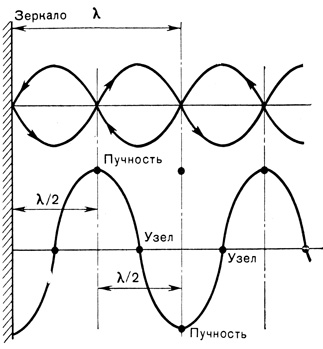
Рис. 32. Схема образования стоячей волны

Следовательно, в точках пучностей концентрируется максимальное количество световой энергии, а в узлах минимальное, причем расстояние между пучностями всегда равно λ/2.

Еще опытами Винера в 1890 году показано, что пучности стоячих световых волн воздействуют па фотоэмульсию, и в тех местах, где пучности пересекались с эмульсией, после проявления возникали почернения, т. е. волны здесь регистрируются фотографически. Винер использовал этот эффект только для измерения длины волны света, однако Липпман пошел дальше.