Цветовые уравнения, графики, пространство, треугольник

Основные цвета делятся на реальные и нереальные. Реальными называются цвета, вызывающие определенные ощущения при действии их на глаз. Нереальные цвета нельзя получить, поскольку нет излучений, вызывающих ощущение таких цветов в нормальных условиях.

Физиологические цвета С, З и К являются нереальными, так как ни одно из реальных излучений не может действовать только на один из трех приемников цветовых ощущений глаза. Поэтому в цветоведении принято реальные основные цвета обозначать буквами R, G, B (англ. Red (красный), Green (зеленый), Blue (синий) (колориметрическая система RGB). В международной колориметрической системе вместо цветов R, G, B берутся другие (реально не существующие) цвета X, Y, Z.

Цветовые координаты определяются двумя способами: измерением на колориметрах и путем расчета по спектральным составам излучений.

Принцип измерения цвета на колориметре показан на рис. 11. На левую грань призмы направляется измеряемое излучение, а на правую - излучение трех основных цветов R, G, B. Регулируя количество излучений R, G, B, добиваются того, чтобы обе грани призмы были освещены одинаково. Таким образом, определяемое излучение состоит из определенного количества излучений красного, зеленого и синего цветов.

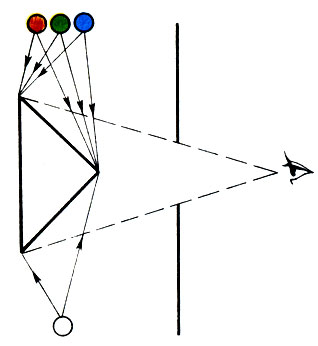
Рис. 11. Принцип измерения цвета на колориметре

В международной колориметрической системе любой цвет С может быть выражен в виде цветового уравнения

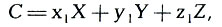
где x₁, y₁, z₁ - цветовые коэффициенты, показывающие, в каких соотношениях должны быть смешаны основные цвета, чтобы получить данный цвет. Для определения цветности, являющейся производной цветового тона и насыщенности, пользуются относительными величинами координат x, y, z₁, которые вычисляются следующим образом:

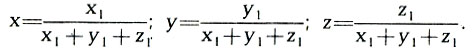
Если сложить три уравнения, можно сделать вывод, что сумма трех коэффициентов равна единице, т. е. x+y+z=1. Значит, если известны два относительных коэффициента (например, x и y), то третий может быть определен по формуле

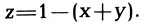
Например, x=0,33; y=0,33; z≈1-(0,33+0,33)≈0,33. Тогда цветовое уравнение может быть записано так: C≈0,33X+0,33Y+0,33Z. Отсюда видно, что синий, зеленый и красный цвета смешаны в одинаковых количествах и цвет смеси будет белым.

Любой цвет может быть изображен графически. Пространственный цветовой график, где в качестве основных цветов взяты синий, зеленый и красный, показан на рис. 12. Из графика видно, что при попарном смешении основных цветов в равных количествах получаются следующие цвета: смесь красного (К) и зеленого (З) - желтый (Ж); красного и синего - пурпурный (П); синего и зеленого - голубой (Г). Цвета Ж₁, П₁ и Г₁ имеют одинаковую цветность (цветовой тон и насыщенность) с цветами Ж, П и Г, но отличаются от них меньшей яркостью. Если же два основных цвета смешиваются не в одинаковых количествах, то получаются другие цвета, например, при преобладании красного цвета при смешении красного и зеленого - оранжевые цвета, а преобладании синего при смешении его с красным - фиолетовые. При смешении всех трех цветов в одинаковых количествах получаются серые цвета различной светлоты - от черного (при отсутствии цветов) до белого (при наибольшем количестве основных цветов). Линия серых цветов ЧБ на графике называется ахроматической осью. Чем больше насыщенность цвета, тем дальше его точка находится от линии ЧБ, и наоборот.

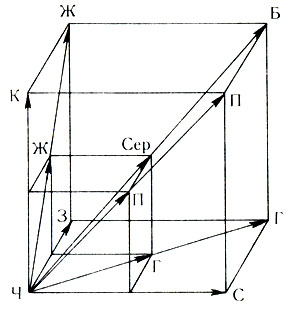
Рис. 12. Пространственный цветовой график

Цветовой график XYZ, полученный с помощью желтой, пурпурной и голубой красок во всевозможных сочетаниях, показан на рис. 13. Пользоваться пространственным цветовым графиком для определения характеристик цвета довольно сложно, поэтому в колориметрии пользуются плоским цветовым графиком в виде равностороннего треугольника. Любой цвет, полученный смешением трех основных, может быть изображен точкой внутри равностороннего треугольника, имеющего высоту, равную единице. Это положение вытекает из правила, что сумма перпендикуляров, опущенных из любой точки, находящейся внутри равностороннего треугольника, на его стороны, равна его высоте. В вершинах цветового треугольника расположены основные цвета (рис. 14). Если взять любой цвет, изображенный в виде точки внутри цветового треугольника и полученный смешением трех основных цветов, то, опустив перпендикуляры на противоположные стороны, легко определить его относительные цветовые коэффициенты, так как сумма перпендикуляров равна единице.

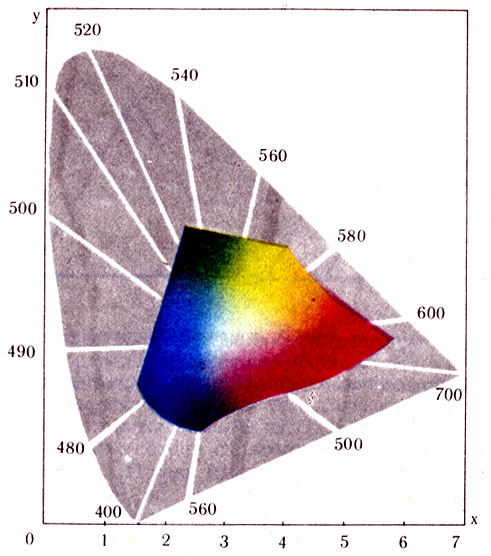
Рис. 13. Цветовой график XYZ

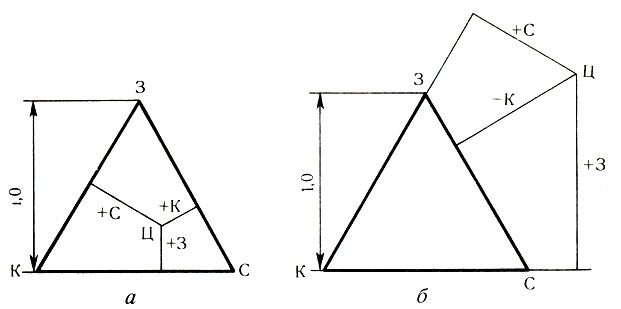
Рис. 14. Определение цвета с помощью цветового треугольника

Цвет, полученный смешением двух основных цветов, лежит на стороне треугольника, соединяющей эти цвета, и делит сторону на отрезки, обратно пропорциональные количествам смешиваемых цветов (рис. 15). Если смешиваются одинаковые количества синего и красного цветов, то получается чистый пурпурный цвет П и точка его делит сторону треугольника пополам, т. е. СП₁=П₁К. Если смешиваются неодинаковые количества синего и красного цветов (красного больше), то получается пурпурный цвет П₂, точка которого делит сторону треугольника на неравные части СП₂>П₂К, обратно пропорциональные количествам синего и красного цветов. В данном случае в смеси преобладает красный цвет и точка П₂ расположена ближе к точке К.

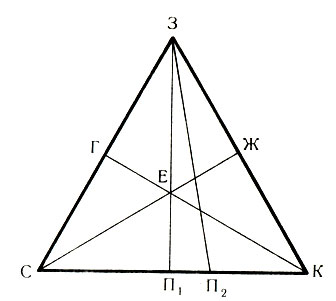
Рис. 15. Определение дополнительных цветов с помощью цветового треугольника

Таким образом, точки на сторонах треугольника представляют собой цвета, полученные смешением двух основных цветов, а внутри треугольника - трех. К последним относится и точка Е, которая представляет цвет, полученный смешением трех основных цветов в равных количествах (точка белого цвета или точка серых цветов), и располагается в центре тяжести цветового треугольника.

Точки дополнительных цветов располагаются в основании перпендикуляров, опущенных на противоположные стороны и проходящих через точку Е. Эти перпендикуляры делят противоположные стороны пополам, следовательно, основные цвета смешиваются в равных количествах.

Цвета, которые не могут быть получены непосредственным смешением основных цветов, располагаются вне цветового треугольника (рис. 14, б). В этом случае перпендикуляры, опущенные на стороны треугольника или их продолжения, являются соответствующими относительными цветовыми коэффициентами и их сумма равна единице, но один из них имеет отрицательное значение (в данном случае - К).